Nel 1967 Amdahl mise a punto una relazione allo scopo di definire, da un punto di vista analitico, l’incremento di prestazioni ottenibile da un sistema di elaborazione multiprocessore.
L’incremento delle prestazioni è direttamente relazionabile con la quantità di microprocessori in gioco? La legge di Amdhal vuole proprio dare una risposta a questa domanda.
È possibile che esiste una relazione tra l’incremento di un elemento di una grandezza con quello complessivo del sistema, e in che modo?
Per ricavare benefici da una architettura dual-core è necessario capire se la propria applicazione è, in un certo senso, parallelizzabile.
Un carico di lavoro può essere diviso in una parte tipicamente seriale e una parallela: la parte parallela deve essere eseguita in ambito multiprocessore, mentre la componente seriale viene posta a carico di un singolo processore.
Se da un sistema volessimo ottenere maggiori prestazioni distribuendo il calcolo su diversi processori, quanti CPU dovremmo definire?
Purtroppo non è che se mettiamo 16 processori allora ricaviamo un risultato sedici volte superiore a quello di una singola CPU.
Per fare delle utili considerazioni dobbiamo tenere conto della legge di Amdahl.
In poche parole non è il numero dei processori che incide in maniera sostanziale all’aumento della velocità, ma un aspetto rilevante, non secondario, è la definizione dell’algoritmo utilizzato: più efficiente è l’algoritmo è più incide sulla relazione.
Il calcolo parallelo ha la sua convenienza se vengono utilizzate non troppi microprocessori o se viene utilizzata una relazione con porzioni di calcolo seriali ridotte.
La relazione di Amdahl viene espressa in questo modo:
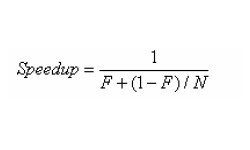con F viene rappresentata la parte sequenziale, (1-F) è la porzione che può essere parallelizzata e N il numero dei processori.
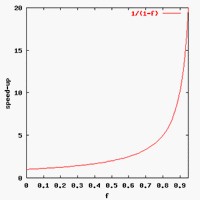
Dalla relazione è possibile accorgersi che per grandi numeri di processori l’accelerazione tende a 1/F.
Questa è una relazione ideale e può aiutare per definire il numero di processori da utilizzare in un sistema; purtroppo non tutti i problemi, nei casi reali, possono essere parallelizzati in maniera da ottenere dei benefici dal calcolo parallelo.
